摘要(yào)：從 電磁(ci)流量計(ji) 理論出(chu)發,建立(lì)插入式(shì)電磁流(liu)量計 的(de)物理模(mó)型,求出(chū)相應的(de)電勢、磁(cí)勢和權(quan)函數的(de)分布,并(bing)💃進行了(le)定量計(ji)算,分析(xi)不同流(liu)場下插(cha)入式電(diàn)👄磁流量(liàng)計的輸(shu)出電勢(shì)差。計算(suan)研究表(biao)明,如果(guǒ)把電極(ji)放置💜于(yu)平均流(liu)速點位(wèi)置,這種(zhong)流量計(jì)可以測(cè)得♻️通過(guo)管道的(de)流量,電(dian)✔️極位置(zhi)偏🐉差所(suǒ)産生的(de)測量相(xiang)對誤差(cha)約爲1%～ 2%。
0引(yǐn)言
　　電磁(cí)流量計(ji)是一種(zhǒng)重要的(de)測量導(dǎo)電性液(yè)體體積(jī)❓流量的(de)儀表,在(zài)城市用(yòng)水、工業(yè)廢水、漿(jiāng)液測量(liang)及食品(pin)等多方(fang)面得到(dào)廣泛應(ying)🍓用。但是(shì)高精度(dù)的電磁(cí)流量計(jì)價格昂(ang)貴㊙️,特别(bie)是大管(guan)徑的,不(bú)僅加工(gōng)困難,而(er)且給安(an)裝、維修(xiū)帶來很(hen)多不便(bian)。因此,在(zai)大管徑(jing)管道🐉的(de)流量測(cè)量方面(mian)常使用(yòng)插入式(shi)電磁流(liu)量計代(dài)替傳統(tǒng)的管道(dào)式流量(liàng)計。本文(wen)從流量(liàng)計理論(lùn)出發研(yan)究該插(chā)入式流(liú)量㊙️計的(de)特性與(yu)可行性(xing)。
1電磁流(liu)量計測(ce)量理論(lùn)
描述電(diàn)磁流量(liang)計的積(ji)分式由(you)Bevir在1970年給(gei)出:

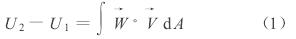
　　式中(zhong):U2- U1是兩電(dian)極之間(jiān)的電勢(shi)差; A表示(shì)對所有(you)的空間(jian)積分; `W稱(chēng)爲矢量(liang)權函數(shù),是一個(gè)隻有電(diàn)磁流量(liàng)計本身(shen)結🌈構決(jue)定的量(liang),其♌表達(dá)式爲:

　　由(yóu)以上分(fen)析可知(zhi),電勢差(cha)的測量(liang)不受流(liú)體的溫(wen)度🔞、壓力(li)、密度、電(diàn)導率(高(gao)于某阈(yu)值)變化(hua)的影響(xiang),具有很(hen)大的🏃‍♂️優(you)越性。
2插(cha)入式電(dian)磁流量(liang)計的理(lǐ)論計算(suan)
　　典型的(de)插入式(shi)流量計(ji)結構如(rú)圖1所示(shì),将電極(jí)插入😘管(guan)道内,磁(cí)極留在(zai)管道外(wài),在電極(jí)周圍産(chǎn)生一個(gè)局部磁(cí)場。


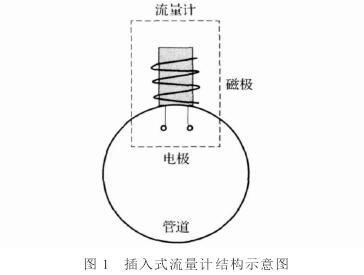
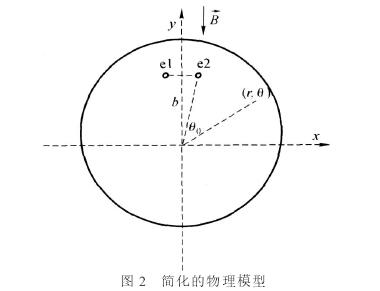
　　建立(lì)物理模(mó)型如圖(tu)2所示:e1、e2爲(wei)插入管(guǎn)道的兩(liǎng)個電極(ji),電極位(wei)置由插(chā)入深度(du)b以及電(diàn)極開角(jiao)θ0決定,`B是(shi)由外部(bu)磁極産(chǎn)生的磁(ci)場。基于(yú)此模型(xing),計算G、F、W的(de)分布。
2.1虛(xu)電勢G的(de)計算
　　由(you)于管道(dào)内有插(cha)入的電(dian)極,所以(yi)不能直(zhí)接使用(yong)式(4)的Laplace方(fāng)程求解(jie)🈲虛電勢(shì)。我們可(kě)将該模(mó)型的虛(xu)電勢分(fen)🍉布認爲(wei)是分别(bié)隻有電(diàn)極和邊(biān)界産生(sheng)的虛電(dian)勢的疊(die)加,即G= G0+ Gr。
2.1.1隻(zhī)有電極(ji)的虛電(diàn)勢分布(bù)
　　假設邊(biān)界無窮(qióng)遠,根據(ju)虛電流(liú)的定義(yì)有:

2.1.2隻有(you)邊界的(de)虛電勢(shì)分布

　　這(zhe)是一個(gè)定解條(tiáo)件的Laplace方(fāng)程,使用(yong)分離變(bian)量及傅(fu)立葉系(xi)數♍公式(shì)可進行(háng)求解。由(you)于很難(nán)求得邊(biān)界條件(jian)的解析(xī)解,我們(men)在徑向(xiang)使用差(cha)分方法(fǎ)求得Gr的(de)邊界條(tiáo)件來求(qiu)得Gr的數(shu)值解。
3.2磁(ci)勢F的計(jì)算
　　由于(yu)電極的(de)插入深(shen)度一般(ban)僅爲管(guǎn)道直徑(jìng)的10%～ 12.5%,因此(ci)假設在(zài)電極附(fù)近的磁(cí)感強度(du)是均勻(yun)的,即：

　　與(yu)求得的(de)W在二維(wéi)圓面内(nei)做數值(zhí)積分即(ji)可求得(de)輸⭐出電(dian)✍️勢差👌U。
3編(bian)程計算(suàn)
　　綜合上(shang)述讨論(lùn)可以看(kan)出,問題(tí)的關鍵(jiàn)在于虛(xu)電勢函(han)數G的計(ji)算,考慮(lü)到精度(du)要求以(yi)及資源(yuan)消耗,使(shǐ)用離散(sàn)方法計(jì)算G。具體(tǐ)實現‼️步(bù)驟如下(xià):
1)将感興(xìng)趣的區(qū)域在二(er)維直角(jiǎo)坐标上(shàng)劃分網(wang)格,使用(yong)式(8)求出(chū)每一微(wei)元上的(de)G0值;
2)使用(yòng)差分方(fāng)法計算(suan)式(9)中邊(biān)界處網(wǎng)格的G0法(fǎ)向方向(xiàng)🌍偏導值(zhí),作爲計(ji)算Gr的邊(bian)界條件(jian);
3)通過分(fen)離變量(liang)、利用傅(fù)立葉系(xì)數公式(shì),以及離(li)散的Simphson積(ji)分⛷️法計(jì)算式(10)得(dé)到Gr的半(ban)解析表(biǎo)達式,計(ji)算每一(yī)網格的(de)Gr值,并⁉️合(he)成G;
4)按照(zhao)式(13)計算(suan)G在x方向(xiàng)的差分(fèn),求得每(měi)一網格(gé)的W值;
5)結(jie)合式(14)的(de)流場模(mo)型,計算(suan)輸出電(diàn)壓。編寫(xie)程序計(ji)算不同(tong)🧑🏽‍🤝‍🧑🏻流✉️場,不(bú)同電極(jí)位置的(de)輸出電(diàn)壓,并繪(huì)制G、W的等(děng)勢分布(bu)圖。
4結果(guǒ)與分析(xi)
4.1虛電勢(shi)G分布(取(qu)電極間(jiān)距爲0.1R)
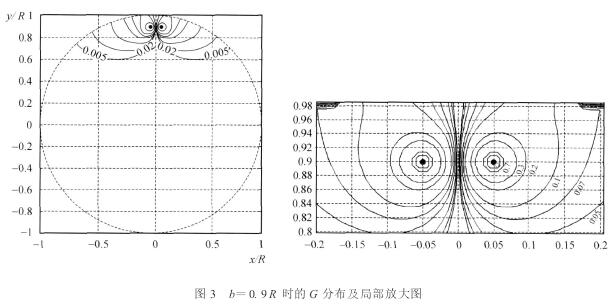
　　取(qu)b= 0.9R(R爲管道(dao)半徑),θ= 0.0555rad,繪(huì)制G分布(bu)并放大(da)電極附(fu)近區域(yù)如圖3所(suo)示。
　　圖3中(zhong)的黑點(diǎn)爲電極(ji),可以明(míng)顯的看(kàn)出G主要(yao)分布在(zai)電極周(zhou)圍♋并🛀且(qie)在邊界(jiè)處分布(bù)發生顯(xiǎn)著的變(biàn)化。
4.2權函(han)數W分布(bu)(取電極(jí)間距爲(wèi)0.1R)
取b= 0.9R,θ= 0.0555rad,繪制(zhì)W分布如(rú)圖4所示(shì)。


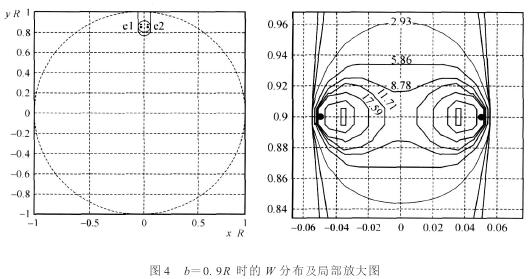
　　從圖4中(zhong)可以看(kàn)出W主要(yao)分布在(zài)電極附(fu)近,并且(qiě)成對稱(cheng)分布。
4.3輸(shu)出電勢(shì)差
　　通過(guò)計算可(ke)以發現(xian),權函數(shù)W主要分(fèn)布在電(dian)極附近(jin)🌈。選擇b= 0.752R,對(duì)`W·` V進行全(quán)空間積(jī)分,求得(de)輸出電(dian)勢差U= 0.1475V(爲(wei)規一起(qǐ)見,假定(ding)❓vmax= 1m/s, R= 1m,電極處(chù)B= 1T);對距離(li)電極所(suǒ)在圓周(zhou)0.05R的環狀(zhuàng)區🚩域進(jin)行積分(fèn),求🥰得輸(shū)出♉電勢(shi)差U= 0.1231。因此(cǐ),對🥰最終(zhōng)輸出電(dian)勢差起(qǐ)作用的(de)主要是(shì)電極附(fù)近的流(liú)場。說明(míng)我們假(jiǎ)設的磁(cí)場模型(xíng)是可用(yong)的。
1156-10在不(bú)同的插(chā)入深度(du)對于不(bú)同的湍(tuān)流系數(shu)n進行求(qiú)💔
解,得到(dào)結果如(ru)表1所示(shi)。

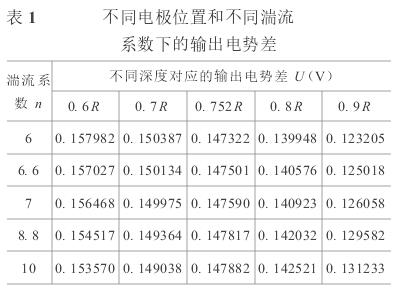
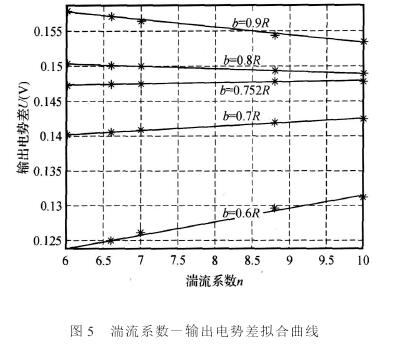
　　繪制湍(tuān)流系數(shù)-輸出電(diàn)勢差曲(qǔ)線如圖(tu)5所示。

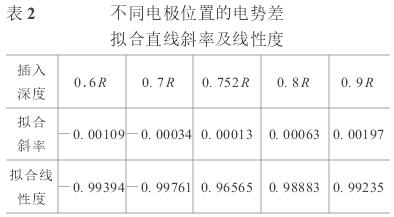
　　對各組(zu)數據做(zuò)最小二(er)乘拟合(hé),計算斜(xié)率及線(xian)性度如(rú)✌️表2所示(shi)。

　　由圖5可(ke)以看出(chu),取vmax= 1,即同(tong)一流量(liàng)下,不同(tóng)的湍流(liu)系數n對(dui)應了不(bú)同的輸(shu)出電壓(yā)。但當b=0.752R,也(yě)就是常(chang)說的平(ping)均流速(su)點位置(zhì),輸出的(de)電勢差(chà)U值基本(ben)不變。因(yīn)此,隻要(yao)♊将電極(ji)插至該(gai)🐆位置,即(ji)🐇可用來(lái)測量流(liú)量。爲了(le)研究插(cha)入深度(dù)偏離平(ping)均🌈流速(su)點所🔴産(chan)生的測(cè)量誤差(cha),假設平(ping)均流速(su)點位置(zhi)的輸出(chu)電勢差(cha)爲标準(zhun)值,計算(suan)🔆得到:插(chā)入深度(dù)與平均(jun)流速點(diǎn)偏差在(zai)0.1R範圍内(nei),輸出電(diàn)勢與該(gāi)标準值(zhi)的相對(duì)✔️誤差約(yuē)爲1%～ 2%。
5結論(lùn)
本文完(wan)成了以(yi)下工作(zuo):
1)建立了(le)插入式(shi)電磁流(liu)量計的(de)物理模(mo)型,并編(biān)寫程序(xu)🐇計算出(chu)虛電勢(shì)、權函數(shu)的數值(zhi)解,用于(yú)指導插(chā)入式電(dian)磁流📱量(liàng)計的實(shi)際生産(chǎn)與運用(yòng);
2)引入經(jing)典湍流(liú)模型,對(duì)不同湍(tuān)流系數(shù),不同電(dian)極位置(zhi)的輸出(chū)電壓進(jin)行模拟(ni)計算,給(gěi)出關系(xi)曲線,從(cóng)理✂️論上(shang)給出電(dian)極🔅最優(you)工作位(wei)置。希望(wàng)在進一(yī)步的工(gong)✏️作中能(neng)加工制(zhi)😄作出插(cha)入式流(liu)量計的(de)實物,通(tong)過流量(liàng)标定實(shí)驗來驗(yàn)證理論(lun)分析結(jié)果。

以上(shang)内容來(lái)源于網(wǎng)絡，如有(you)侵權請(qǐng)聯系即(jí)删除!